【python数据挖掘案列】利用线性回归(LR)实现天气变化的时间序列预测

云天徽上 · 发布于 2024-7-5 18:24:27

利用线性回归实现天气变化的时间序列预测

一、引言

天气预测一直是气象学和机器学习领域的重要研究内容。时间序列预测是其中的一种常见任务，旨在通过分析历史数据来预测未来的天气情况。在本文中，我们将使用线性回归模型来实现天气变化的时间序列预测，并介绍整个预测流程。

二、加载数据

首先，我们需要一个包含天气数据的数据集。假设我们有一个CSV文件，其中包含了过去几年的每日天气数据，如温度、湿度、风速、气压等特征，以及我们想要预测的下一日的某个天气指标（如温度）。

import pandas as pd

# 加载数据
data = pd.read_csv('weather_data.csv')
data.head()

请确保CSV文件中的数据格式正确，并且已经按照日期进行了排序。

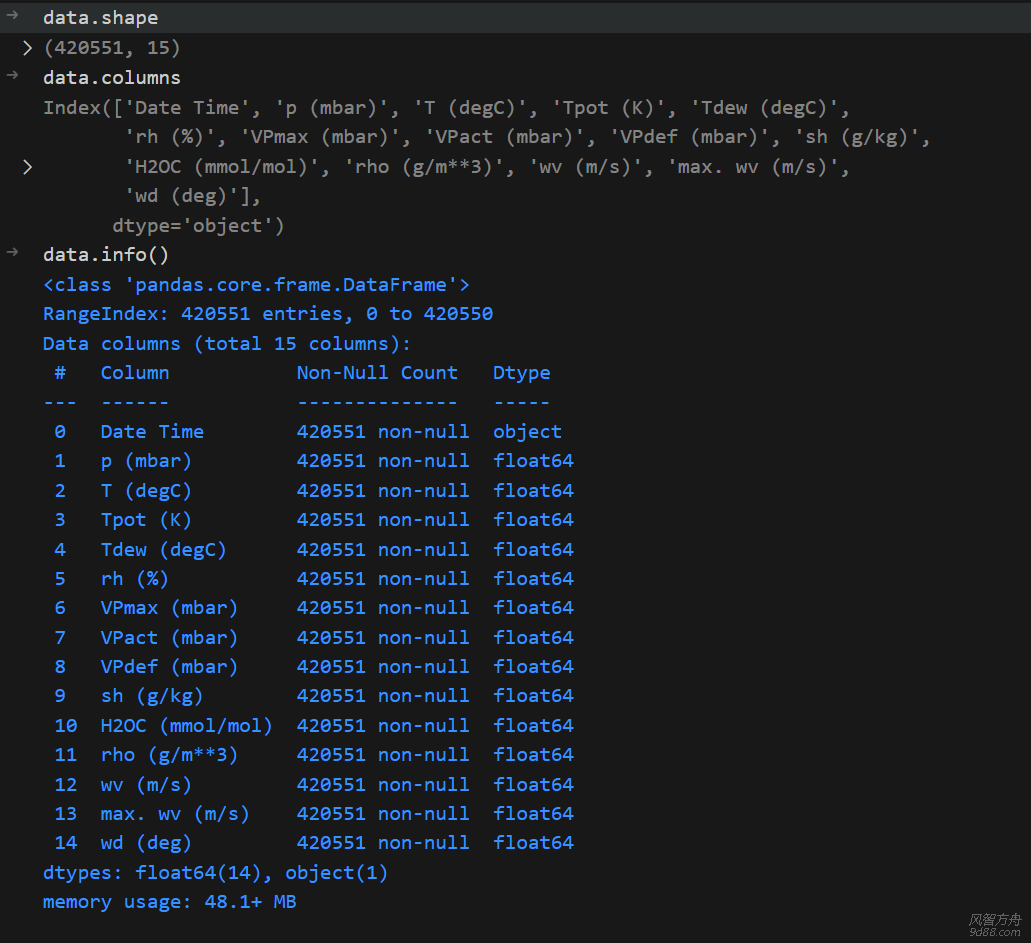
下面是对每个特征的简要介绍：

Date Time：日期和时间，表示数据记录的具体时间点。
p (mbar)：气压（以毫巴为单位）。气压是大气对地球表面单位面积上的垂直压力，是天气系统的一个重要参数。
T (degC)：温度（摄氏度）。表示空气的温度，是气象观测的基本要素之一。
Tpot (K)：位温（开尔文）。位温是考虑了气压对温度影响后的一个热力学温度，常用于热力学计算中。
Tdew (degC)：露点温度（摄氏度）。露点温度是空气在水汽含量和气压都不改变的条件下，冷却到饱和时的温度。低于此温度时，空气中的水蒸气会凝结成水。
rh (%)：相对湿度（百分比）。相对湿度表示空气中水蒸气含量接近饱和的程度，是描述空气湿度的一个重要参数。
VPmax (mbar)：最大水汽压（毫巴）。在给定的温度下，空气所能容纳的水汽压的最大值。
VPact (mbar)：实际水汽压（毫巴）。当前空气中实际存在的水汽压。
VPdef (mbar)：水汽压亏缺（毫巴）。表示空气未达到饱和状态的水汽压差值，即VPmax与VPact之差。
sh (g/kg)：比湿（克每千克）。比湿是空气中水汽质量与湿空气总质量的比值，用于描述空气的湿度。
H2OC (mmol/mol)：水汽浓度（毫摩尔每摩尔）。表示空气中水蒸气分子的浓度，是另一个描述空气湿度的参数。
rho (g/m3)**：密度（克每立方米）。空气的密度，与温度、压力和湿度等因素有关。
wv (m/s)：风速（米每秒）。表示空气流动的速度，是描述风况的基本参数。
max. wv (m/s)：最大风速（米每秒）。在给定的时间窗口内观测到的最大风速。
wd (deg)：风向（度）。风向是指风吹来的方向，通常用角度表示，从正北方向开始顺时针度量。

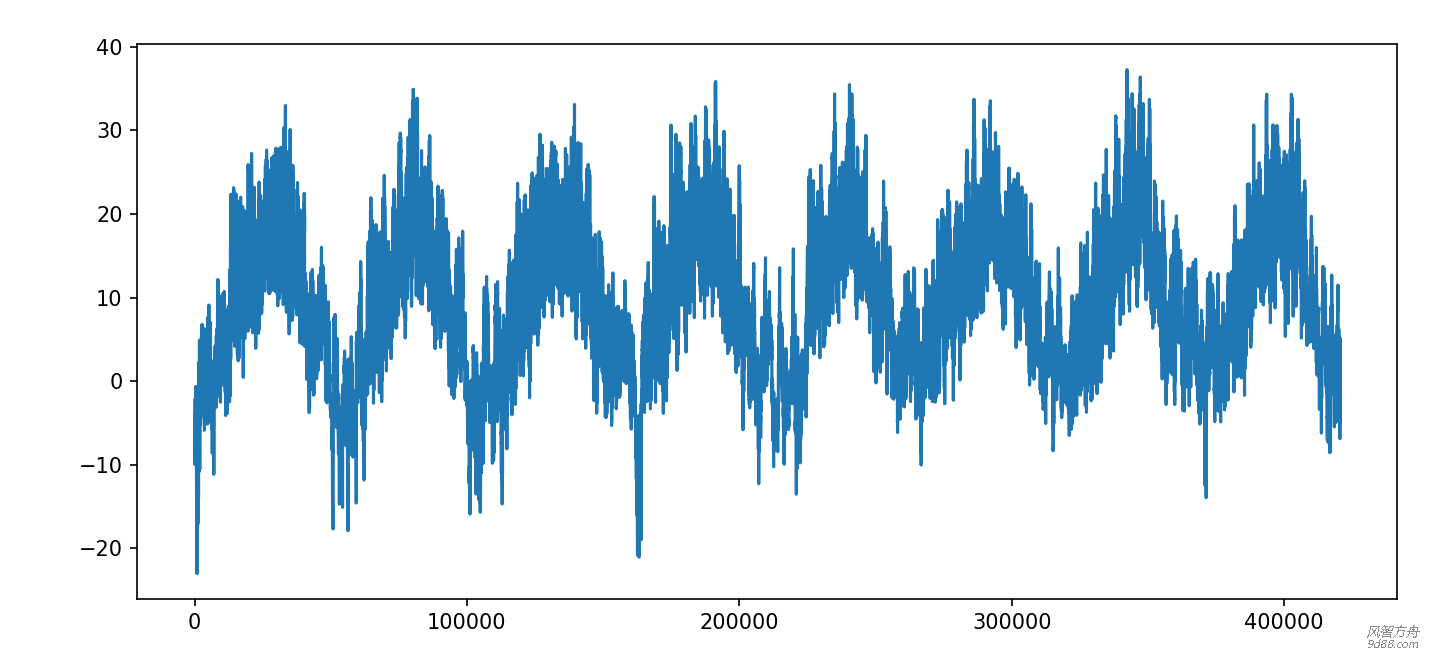
三、将数据进行标准化

在机器学习模型中，通常需要对数据进行标准化处理，以消除不同特征之间的量纲差异，提高模型的训练效果。

from sklearn.preprocessing import StandardScaler

# 选择特征列,不考虑其它列的特征，后续优化时可以采用，包扩特征工程产出的特征；
features = ['T (degC)',  'rh (%)', 'wv (m/s)', 'p (mbar)']
scaler = StandardScaler()
data[features] = scaler.fit_transform(data[features])

四、形成训练数据

在时间序列预测中，我们需要使用历史数据来预测未来的天气情况。因此，我们需要将数据组织成适合模型训练的形式。

# 假设'date'是日期列，'target_temperature'是我们要预测的目标温度
def create_lag_features(data, lag_start=1, lag_end=7):
    lags = {}
    for i in range(lag_start, lag_end+1):
        lags[f'lag_{i}'] = data[['date', 'target_temperature']].groupby('date').shift(i)['target_temperature']
    return pd.concat([data, pd.DataFrame(lags)], axis=1)

# 创建滞后特征
data = create_lag_features(data)

# 删除缺失值和无法预测的数据行
data.dropna(inplace=True)

# 划分特征和目标变量
X = data.drop(['date', 'target_temperature'], axis=1)
y = data['target_temperature']

这里我们假设使用过去7天的温度数据作为特征来预测下一天的温度。

五、划分训练集和测试集

为了评估模型的性能，我们需要将数据集划分为训练集和测试集。

from sklearn.model_selection import train_test_split

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

六、定义模型

在本例中，我们将使用线性回归模型进行预测。

from sklearn.linear_model import LinearRegression

# 定义线性回归模型
model = LinearRegression()

七、模型训练

使用训练数据对模型进行训练。

# 训练模型
model.fit(X_train, y_train)

八、训练集、测试集验证

在训练完成后，我们需要对模型进行评估，以验证其在未见过的数据上的性能。

# 在训练集上进行预测
y_pred_train = model.predict(X_train)

# 在测试集上进行预测
y_pred_test = model.predict(X_test)

# 计算均方误差（MSE）和平均绝对误差（MAE）
mse_train = mean_squared_error(y_train, y_pred_train)
mae_train = mean_absolute_error(y_train, y_pred_train)
mse_test = mean_squared_error(y_test, y_pred_test)
mae_test = mean_absolute_error(y_test, y_pred_test)

print(f'训练集MSE: {mse_train:.4f}, MAE: {mae_train:.4f}')
print(f'测试集MSE: {mse_test:.4f}, MAE: {mae_test:.4f}')

九、参数调优（网格搜索）

虽然线性回归模型的参数较少，但我们仍然可以使用网格搜索来寻找最优参数（尽管在这个例子中可能并不明显）。但在实际应用中，如果我们使用的是更复杂的模型（如随机森林、梯度提升机等），网格搜索将变得非常有用。

from sklearn.model_selection import GridSearchCV

# 对于线性回归，通常没有太多参数可以调整，但我们可以尝试调整正则化参数（如果使用了岭回归或Lasso）
# 但这里，为了示例，我们仅演示结构，并不实际运行网格搜索

# 假设我们使用岭回归（Ridge Regression）
from sklearn.linear_model import Ridge

# 定义参数网格
param_grid = {'alpha': [0.1, 1, 10]}

# 创建岭回归模型
ridge_model = Ridge()

# 创建网格搜索对象
grid_search = GridSearchCV(estimator=ridge_model, param_grid=param_grid, cv=5)

# 注意：这里我们不会实际运行网格搜索，因为对于线性回归来说，它可能不是必要的
# 如果运行，将使用如下代码：
# grid_search.fit(X_train, y_train)
# best_params = grid_search.best_params_
# best_score = grid_search.best_score_

# 输出最佳参数和得分（此部分代码在实际运行网格搜索后才有意义）
# print("Best parameters found:", best_params)
# print("Best score found:", best_score)

十、绘制结果

为了直观地了解模型的性能，我们可以绘制实际值和预测值的对比图，以及模型的残差图。

import matplotlib.pyplot as plt

# 绘制训练集和测试集的预测结果
plt.figure(figsize=(12, 6))
plt.scatter(range(len(y_train)), y_train, color='blue', label='Train True')
plt.scatter(range(len(y_train), len(y_train) + len(y_test)), y_test, color='red', label='Test True')
plt.plot(range(len(y_train)), y_pred_train, color='green', label='Train Pred')
plt.plot(range(len(y_train), len(y_train) + len(y_test)), y_pred_test, color='orange', label='Test Pred')
plt.xlabel('Observation')
plt.ylabel('Temperature')
plt.legend()
plt.show()

# 绘制残差图（仅针对测试集）
plt.figure(figsize=(12, 6))
plt.scatter(range(len(y_test)), y_test - y_pred_test, color='purple')
plt.hlines(y=0, xmin=0, xmax=len(y_test), colors='black', linestyles='dashed')
plt.xlabel('Observation')
plt.ylabel('Residual')
plt.title('Residual Plot')
plt.show()

在残差图中，我们希望看到所有的点都紧密地围绕在水平线上，这表示模型的预测误差较小。

总结

在本文中，我们介绍了如何使用线性回归模型进行天气变化的时间序列预测。虽然线性回归模型在复杂的时间序列预测任务中可能不是最佳选择，但它提供了一个很好的起点，让我们能够了解时间序列预测的基本概念和方法。对于更复杂的任务，可能需要使用更先进的模型和技术。